A brief look at distributions.
Aru Gyani | 03-31-2025

Hey, quick note here. I’m working through The Nature of Code by Daniel Shiffman and taking some notes as I go. This document is just some notes & definitions cobbled together of basic probability concepts that I’ve gotten hazy on over the years. - Aru Gyani
A probability distribution describes how likely different outcomes are in a random process.
There are 2 main types:
Discrete: Outcomes are countable (like rolling a die), e.g.
Continuous: Outcomes are from a continuous range (like height or time), e.g.
Uniform randomness means every possible outcome of a situation has an equal chance of occurring - this is modeled by a uniform distribution.
For example, if you shuffle a deck of cards and pick one, each card has the same chance of being chosen. This is a discrete uniform distribution. These are the most common example you’ll see when talking about uniform distributions.
But that doesn’t mean uniform distributions have to be discrete - they can be continuous too.
Imagine you’re picking a random time between 2:00 and 3:00 PM. Any point in that hour is just as likely to be picked as any other. You’re just as likely to pick 2:34 PM as 2:34:56 PM - or even 2:34:56:7890 PM. This can go on infinitely, which is why we call it a continuous uniform distribution.
If we wanted to turn this into a discrete, we could say: pick a random minute between 2:00 and 3:00 PM. Now we have a finite number of options - 60 minutes - each with an equal chance of being picked.
Non-uniform distributions are distributions where some outcomes are more likely than others; the probabilities are not evenly spread.
Imagine a loaded die where the number 6 comes up more often than the rest. Some outcomes have higher chances than others.
Warning: This is not a recommendation to use a loaded die in questionable settings.
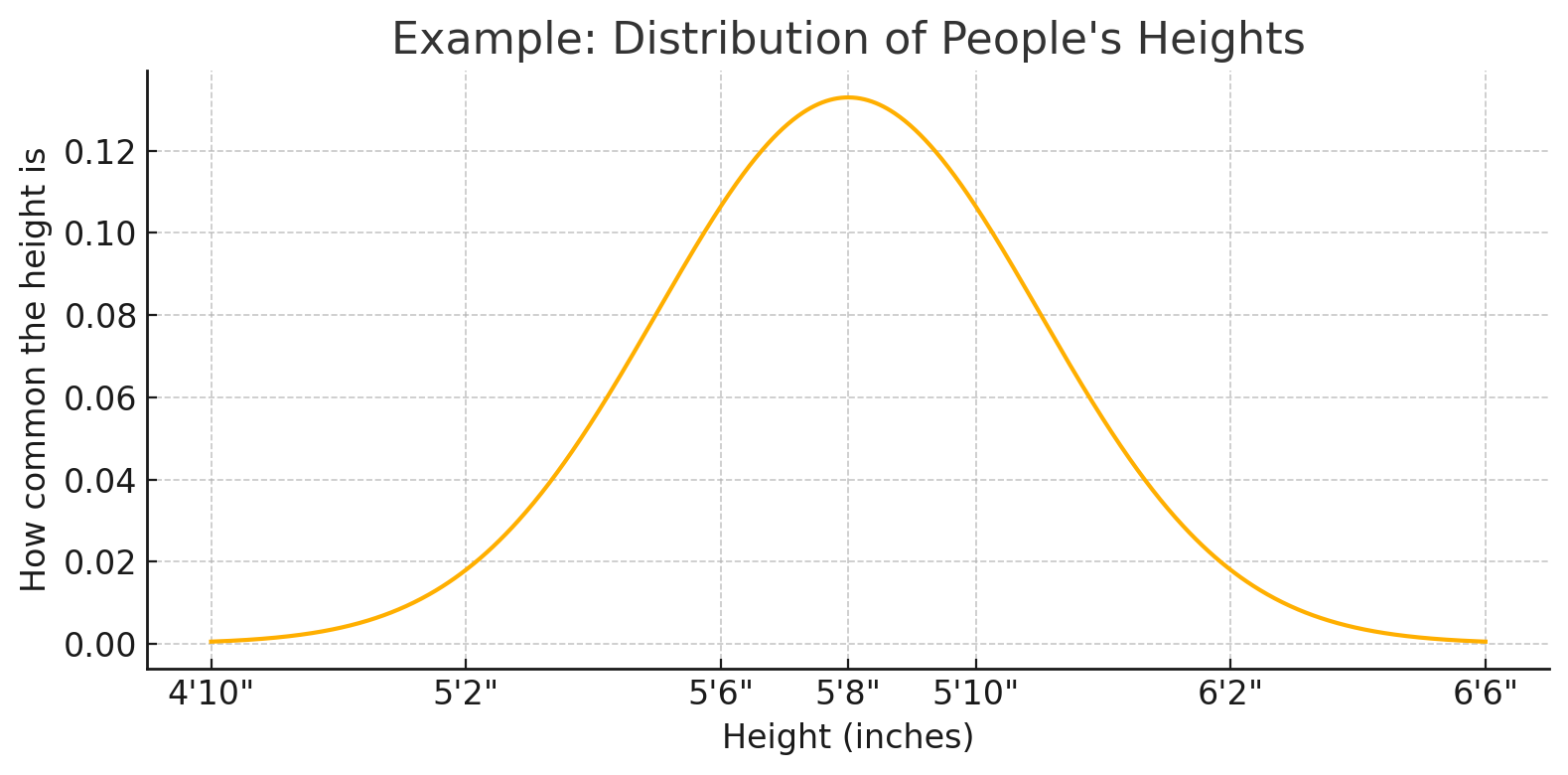
Imagine you lined everyone up by height. Most people would be somwhere in the middle; not too short, not too tall. Only a few people would be really short or really tall. So, some height show up more often than others.
When you measure a large group, you’ll notice that average height shows up the most. As you move farther from the average - say from 5’ 8” to something like 4’ 11” or 6’ 5” - those heights become less common. The pattern you get is smooth and predictable, not just random jumps. This is what we call a continuous non-uniform distribution. You’re dealing with a range of values, and some parts of the range are more common.
This kind of pattern where most values cluster around the average and gradually thin out toward the extremes is often described by a normal distribution. It’s a specific type of continuous non-uniform distribution that’s super common in the real world. Visually, it looks like a smooth, symmetrical, bell-shaped curve. The peak is at the average value, and the curve gently slopes down on both sides, showing how less commong the most extreme values are.

Figure 1: A normal distribution of people's heights
Let’s back up for a second. We’ve used the word outcome a few times already, so what exactly is it? In probability, outcomes are all the possible result of a random process. An outcome (singular) is one specific result. Like rolling a 4 on a die.
Building on that, an event is the specific outcome or group of outcomes you’re interested in. For example, rolling an even number (2, 4, or 6) is an event made up of multiple outcomes.
Single-event probability is the chance or likelihood that one specific outcome will happen in a random process. This might be a bit confusing; didn’t we just say that an event can have multiple outcomes? That’s still true. The key-word here is “single” and it refers to the single trial (e.g. one dice roll, one coin flip, etc.).
What matters is the specific outcome in that trial. This event could be something specific like rolling a 3, or something broader like rolling an even number (2, 4, or 6). In both cases, it’s still single-event probability, because it’s all about what happens in one trial.